Day 5: Heat Engines, Cycles, and Heat Capacities.

Heat Engine Using a Simple Gas Cycle

In class Drawing

Redrawn Cycle

We took the instruction in our lab manual and calculated the change in internal energy, the work, and the heat transferred in each transition of the simple cycle. We first found the energy at each point using E=3/2*P*V. We then calculated the difference between two of the points to find the change in internal energy. The work was calculated using W=P*ΔV for each process. In order to determine Q, we used the first law of thermodynamics Q=ΔE+W. Between points 2 and 3 as well as 4 and 1 there was no work done because there was no change in volume, therefore during these periods ΔE=Q.

Carnot Cycle

In order to set up this cycle we followed the sample Carnot Cycle's instructions in our lab manual. With the given values we were able to calculate E for each point of the cycle. After solving for E we took the difference between two points to find ΔE. A to B and C to D were both isothermal processes, expansion and compression. B to C and D to A were Adiabatic processes, expansion and compression. For the isothermal expansion/compression we found the work using W=n*R*T*ln(V2/V1). Then solved for Q using the First Law of Thermodynamics. For the adiabatic expansion/compression we found the work using the WA equation at the top of the picture. However, considering that during an adiabatic process Q=0 it was simpler t calcuate W by using the ΔE=-W. We also did verify that the system was 33% efficient.

ActivPhysics: 8.7 Heat Capacity

Questions 6 and 7

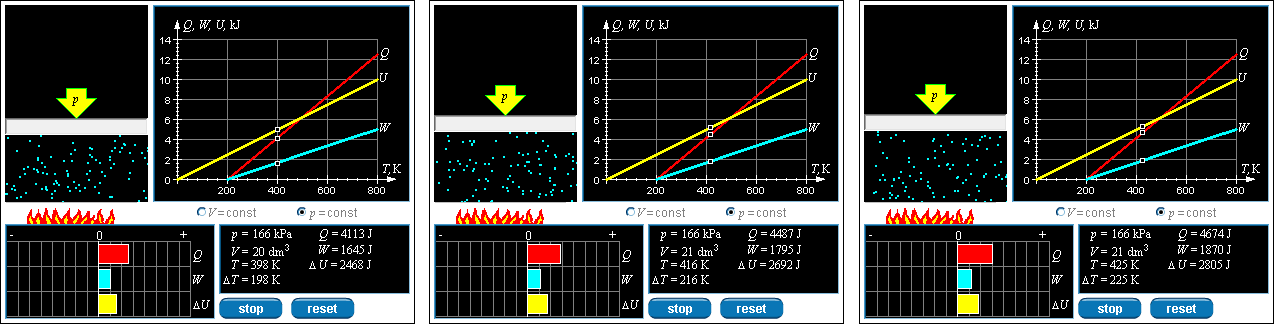
Question 6: Heat and Temperature Change Numbers
RESET the simulation. RUN the simulation and STOP it when the system temperature is about 400K. Record the heat transfer that has already occurred and the present temperature. Then RUN the simulation again and quickly stop it. Record the heat transfer DQ and temperature again. Repeat the process several times. Use the numbers you have obtained to estimate the constant pressure molar specific heat capacity of this ideal gas. When you are finished, compare your answer to that of the Advisor.

---

Question 7: A More Accurate Heat Capacity Measurement
RESET the simulation to bring the temperature to 200K. Note the numbers on the meter. Press RUN and then stop the simulation when the temperature reaches about 800K and note the numbers in the meter. Make an accurate calculation of the constant pressure molar heat capacity of the ideal gas. When you are finished, compare your answer to that of the Advisor.

This time in ActivPhysics we learned about the effects of constant pressure and constant volume on W, Q, and ΔE. Question 6 and 7 in asked us to determine the molar heat capacity at constant pressure. 

Question 8

Question 8: A Theoretical Determination of the Constant-Pressure Molar Heat Capacity of an Ideal Gas

	Apply in symbols the first law of thermodynamics to this process--warming the gas at constant pressure.
	Substitute the expression for the internal thermal energy change of the gas in terms of the temperature change (use only symbols--not numbers).
	Substitute an expression for the work done by the gas in terms of the pressure, the initial volume and the final volume of the gas (use only symbols--not numbers).
	Then use the ideal gas law to rewrite this expression for work in terms of initial and final temperatures and other quantities (symbols only--not numbers).
	Rearrange this last equation so that the left side equals the molar heat capacity at constant pressure. You should have only constants remaining on the right side of the equation. Calculate the value of these constants and compare to your answer in Question 7. Hopefully, the values are the same!

If you have trouble, you can get help from the Advisor.

For this question we mathematically derived the molar heat capacity at constant pressure.