In this activity we used an "Electric Field" of nails and a square metal wire to determine the angle, θ, between the normal vector to the surface and the electric field. When the surface enclosed 49 nails (7x7) the angle between the the normal vector and electric field vector was 0° because the vectors were pointing in the same direction. As we began to enclose less and less nails (42, 35, 28, 21, 14...etc.) the angle between the normal vector and the electric field increased until we enclosed 0 nails and got an angle of 90°. In order to measure the angle of the nails we measured the distance of the diagonal and the height of the wire (see picture below). Using these measurements and trigonometry we were able to solve for the angle between the normal and electric field vectors in both degrees and radians.
After calculating the angles we graphed the Number of Nails (field lines) vs the Angles between the Normal and Electric Field Vectors (radians) in Logger Pro and fit a sine/cosine curve because it best represented the data set. We had trouble getting the curve to properly fit the graph so we manually fit it.
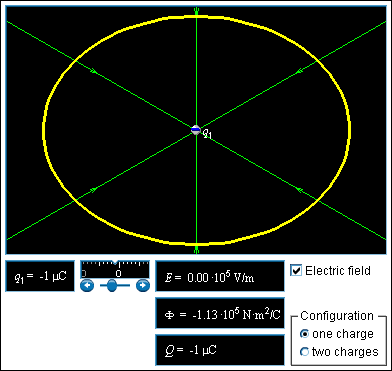
ActivPhysics: 11.7 -- Electric Flux
Question 1: Flux Into or Out of an Oval
Design your own experiments to see how electric charge affects the flux into or out of the oval. In your experiments, you can:
Design your own experiments to see how electric charge affects the flux into or out of the oval. In your experiments, you can:
• change the shape of the oval;
• move the center of the oval so that it surrounds the charge or does not surround the charge; and
• change the magnitude and sign of the electric charge.
When finished, develop in words a qualitative rule to determine the electric flux flowing into or out of the oval. Give examples to support your statements. When finished, compare your thinking with that of the Advisor.
Answer: Based in the images above we concluded that when there was a net positive charge inside of the oval the flux was also positive. If we increased the charge then the flux proportionally increased as well. When the oval had a zero net charge within it, the flux was also zero. When there was a net negative charge inside the oval the flux was also negative. This leads us to believe that flux is proportional to the net charge inside the contained surface.
Question 2: Electric Flux with Two Charges
In the simulation, click the "two charges" configuration. You can now adjust the sign, magnitude and separation of two electric charges. Repeat the experiments such as done in Question 1 to see if your rule applies for this two charge system. You can:
In the simulation, click the "two charges" configuration. You can now adjust the sign, magnitude and separation of two electric charges. Repeat the experiments such as done in Question 1 to see if your rule applies for this two charge system. You can:
• change the shape of the ring;
• change the position of the center of the ring (move it all over); and
• change the magnitudes and signs of the electric charges.
When finished, compare your thinking with that of the Advisor.
Answer: For the case of two charges we found the results to mimic those of the one charge case. If the net charge inside the oval was positive then we got a positive flux. If the net charge was negative there was a negative flux. If the oval didn't surround a charge, or the net charge inside the oval was zero then we had no flux.
Question 3: First way to determine electric flux
Change the simulation back to "one charge." The meter indicates the electric flux Φ into or out of the oval and the net electric charge Q inside the oval.
Change the simulation back to "one charge." The meter indicates the electric flux Φ into or out of the oval and the net electric charge Q inside the oval.
• What happens to the flux if you double or triple the positive electric charge inside the oval?
• What happens to the flux if you double or triple the negative electric charge inside the oval?
• Find an equation with a proportionality constant that relates the electric flux into or out of the oval and the electric charge inside the oval.
After answering the questions, compare your thinking with that of the Advisor.
Answer: When we doubled or tripled the charge we saw that the flux also double or tripled accordingly. If the charge was negative and we increased it by a factor of 3 we saw the flux proportionally triple as well. The same is true for the positive charge. This tells us that flux is directly proportional to the net charge inside of the oval.
Question 4: Second way to determine electric flux
The green electric field lines represent the electric field surrounding the source charges. Develop a rule for the electric flux passing out of or into the oval by counting the electric field lines passing out of or into the oval. After answering the questions, compare your thinking with that of the Advisor.
The green electric field lines represent the electric field surrounding the source charges. Develop a rule for the electric flux passing out of or into the oval by counting the electric field lines passing out of or into the oval. After answering the questions, compare your thinking with that of the Advisor.
Answer: Based on what we've seen thus far the number of flied lines going in/out is directly proportional to the flux.














No comments:
Post a Comment