Day 7: Electric Force

Electric Force Law Video Analysis

For this experiment we were asked to analyze the Coulomb video posted below and determine the charges of the two balls used i the experiment. We were able to determine the charge of each ball with measured values for distance and length (2.00 m), mass (2.93 g), and some trigonometry. 

Experiment

Analysis

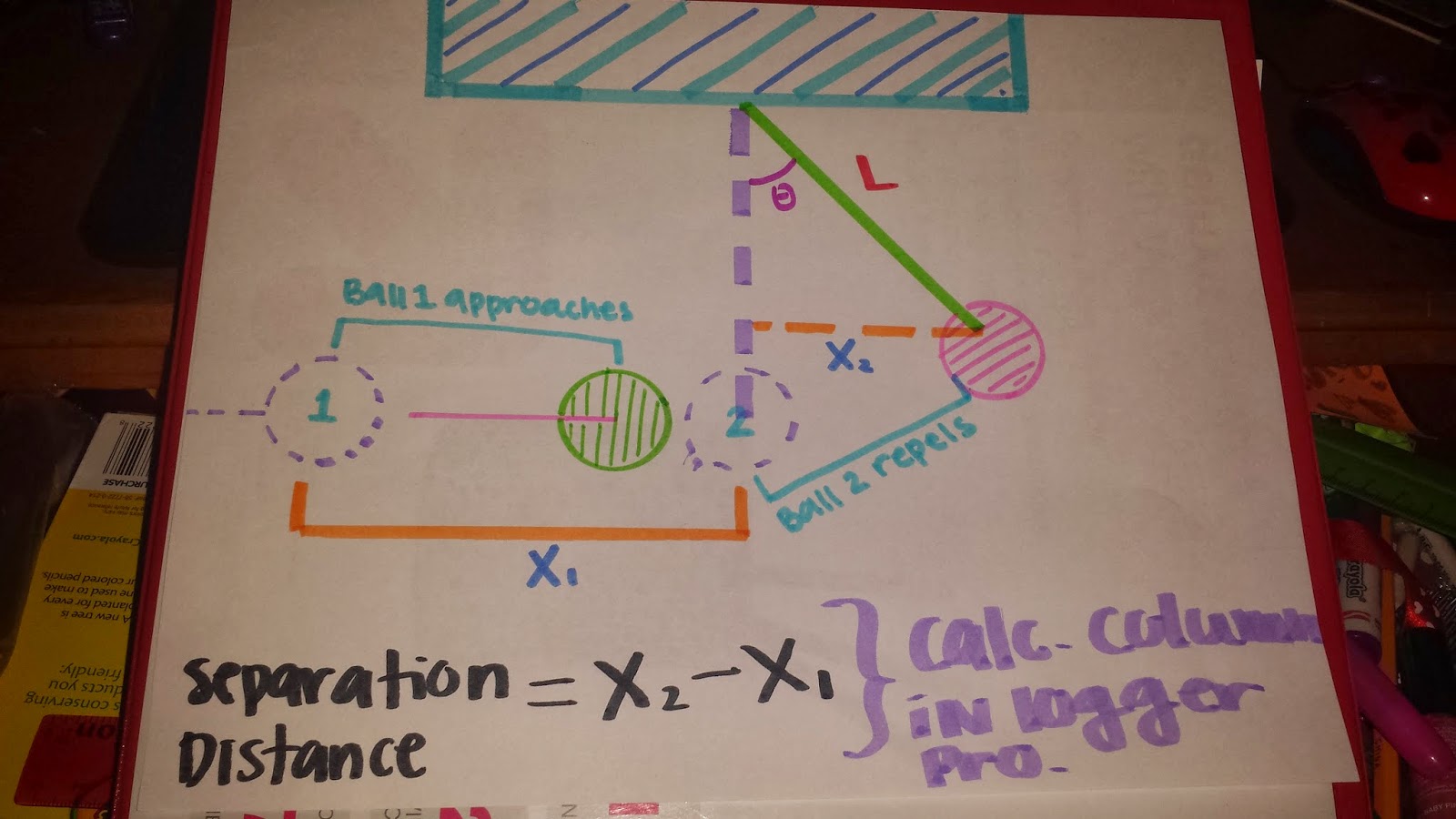
After viewing the video we plotted the movement of each ball with respect to the origin (placed on the hanging ball). Each point helped to determine the values of X1 (the distance between the ball on rod and origin) and X2 (the displacement of the hanging ball from the origin). 

X1 and X2 were crucial values that helped to calculate the separation distance at any given time between the two balls. We imputed the formula X2 - X1 into logger pro as a new calculated column (shown below).

We then used a free body diagram of the forces affecting the hanging ball in order to determine the electric force.

Using what we know about Newtons's Laws. We determined forces in both the X and Y direction and calculated the electric force to be FE=m·g·(tanθ).

Since θ is not a known value in this experiment we could not calculate force with FE=m·g·(tanθ), so we needed to rewrite the formula in terms were given. In this case that meant L, X2, m, or g. With the use of trigonometry and the pythagorean theorem we found a new equation for electric force: FE=m·g·(X2/sqrt(L^2-X2^2)). This formula was used as a new calculated column in logger pro and imputed as shown below. 

After everything was properly input in logger pro we created an Electrical Force vs Separation Distance graph. Our data showed the following result:

The relationship between Electrical Force and Separation Distance turned out to be a inversely proportional (power function was fitted). With our exponent value equaling 1.763.

Conclusion

1. We were able to determine successfully that Electric Force is inversely proportional to the square of the distance between the charges. Based on our graph you can easily see that as the distance between the charges decreases the electric force increases and vice versa.

2. We determined our percent difference between our experimental exponent and the theoretical exponent to be 13.2% (part a). In the scenario where we assumed that the two balls had the same charge (part b), we calculated the charge of each ball to be q=3.91·10^-8 C. In part c where the assumption was made that the charge of the hanging ball was 1/2 that of the other ball we found q2=5.53·10^-8 C and q1=2.76·10^-8 C.

3. From this experiment it is not possible to determine the charges of the ball. All we know for sure is that the sign of the charges for the two balls is the same. Meaning they are both either positively or negatively charged because they repelled when ball 1 approached the hanging ball (ball 2). 

4. Some sources of uncertainty for this experiment include the measurements of distances in logger pro. In order to get the values we had to manually track the movement of the ball and ensure that each time we marked the ball at its center. If this was not done our values might have been slightly off. This would have cause our separations distances to be either higher or lower and give incorrect values for our graph.